Menu
- Accueil /
- Partie Théorique /
- Théorème de Bernoulli pour des fluides réels
Théorème de Bernoulli pour des fluides réels
Énoncé du théorème.
La difference entre un fluide parfait et un fluide réels, c'est l'existance d'une force de viscosité dans le fluide réels.
Donc entre deux points d'énergie d'un écoulement non parfait et incompressible on a une dissipation d'énergie mécanique, appeler "perte de charge".
Dans le cas de l’écoulement d’un fluide réel (viscosité non nulle), il y a des pertes de charges entre deux points A et B.

L’équation de Bernoulli devient alors :
Pa +1/2.ρ.va2 +ρ.g.za =Pb +1⁄2.ρ.vb2 +ρ.g.zb + Δp
Où:
- P : la pression en Pa
- ρ : la masse volumique en g/mol
- v : la vitesse en m/s
- Z : la hauteur en m
- Δp : ensemble des pertes de charge entre (1) et (2). Elle s ’exprime en Pascal (Pa).
On note deux types de pertes de charges d'énergie mécanique :
- perte de charge régulière réparties tout au long d'une conduite
- perte de charge singulière qui apparaissent de manière localisée : dans des coudes, suite à un obstacle, et lors d'un élargissement ou un rétrécissement.
Forces de viscosités.

La pression d'un liquide réel diminue tout au long d'une canalisation dans laquelle il s'écoule, meme
si elle est horizontale et de section uniforme, contrairement au théorème de Bernoulli.
Ce phénomène est du aux forces de frottement qui se nomment forces de viscosité dans le cas d’un
fluide, et s’opposent au glissement des couches fluides les unes sur les autres.
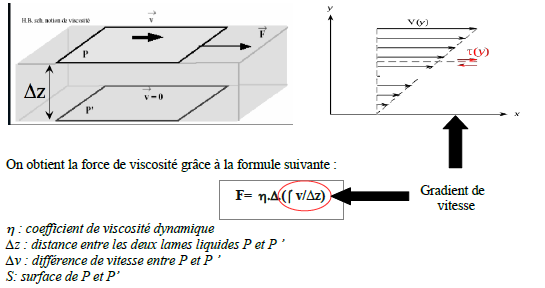
Le coefficient de viscosité dépend du fluide et des conditions physiques dans lesquelles il se trouve.
Unité de η : Pascal . Seconde (Pas.s) ou Poiseuille (Pl)
(1 Pa.s = 1 Pl = 1 kg.m-1.s -1)
Il existe aussi un coefficient de viscosité cinétique tel que :
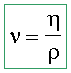
où:
ν : Viscosité cinématique
ρ : masse volumique
Unité de ν : m2.s-1 ou le Stokes (1 St = 104 m2.s-1)
À titre d’exemple, les valeurs de η et ν, à la température ambiante (20 °C) sont :
pour la glycérine : η = 0,8 Pl ν = 6,8 10-4 m2/s
pour l’huile : η = 0,3 Pl ν = 4 10-4 m2/s
pour l’alcool : η = 1,2 10-3 Pl ν = 2,2 10-6 m2/s
pour l’eau : η = 10-3 Pl ν = 10-6 m2/s
pour l’air : η = 18 10-6 Pl ν = 15 10-6 m2/s
Différents régimes d’un écoulement.
En mécanique des fluides on distingue deux grands types d'écoulement :
– l'écoulement laminaire : les lignes de courant sont toujours bien définies. La viscosité du fluide régit l'écoulement et a le temps d'agir.
– l'écoulement turbulent : Des tourbillons apparaissent et les lignes de courant ne sont pas toujours définies. L'effet de viscosité est quasi-négligeable, elle n'a pas le temps d'agir.

On appelle « vitesse débitante » la vitesse moyenne d'entrée définie comme :
Vmoy=Qv/S
Où: Q: débit volumique en m3/s
S: la surface de la section en m2
Pour définir si un écoulement est laminaire ou turbulent il faut calculer le nombre de Reynolds :

Si Re ≤ 2000 l'écoulement est laminaire
Si Re ≥ 3000 l'écoulement est turbulent

Écoulement laminaire et pertes de charge régulières.
Partons de l'équation de Navier-Stokes établie pour l'écoulement d'un fluide newtonien incompressible :
![]()
Si l'écoulement est stationnaire, la dérivée particulaire se résume à la dérivée convective et peut se développer comme :
![]()
On peut alors écrire :
![]()
L'accélération de la pesanteur dérivant d'un potentiel et le fluide étant incompressible, on regroupe sous un même gradient trois des cinq termes de cette équation pour lui donner la forme suivante :
![]()
On retrouve ainsi une formulation semblable à celle conduisant pour un fluide parfait à l'équation de Bernoulli. De la même manière, le produit vectoriel de la vectrice vitesse avec le rotationnel de la vitesse s'annule lorsque l'équation est considérée sur l'ensemble des points constituant une ligne de courant. Il reste donc que le long d'une ligne de courant, l'écoulement stationnaire d'un fluide de viscosité non négligeable obéit à l'équation suivante :
![]()
La pression totale (également appelée « charge »), notée![]() , correspond à la somme des trois termes de pression se trouvant sous le gradient :
, correspond à la somme des trois termes de pression se trouvant sous le gradient :
![]() .
.
C'est donc une quantité scalaire qui doit vérifier l'équation :
![]()
Un écoulement laminaire étant caractérisé par un champ de vecteurs vitesse tous orientés dans la même direction, supposons qu'un repère cartésien soit choisi de telle sorte qu'en tout point de l'écoulement on ait ![]() . Dans ces conditions, la projection dans les trois directions du repère de l'équation précédemment établie, donne :
. Dans ces conditions, la projection dans les trois directions du repère de l'équation précédemment établie, donne :
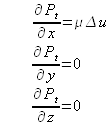
On en déduit que la pression totale n'est fonction que de ![]() , et qu'elle varie en obéissant à l'équation :
, et qu'elle varie en obéissant à l'équation :
![]()
Par ailleurs, l'écoulement étant conservatif, l'équation de continuité s'applique dans sa forme la plus simple :
![]()
et comme ![]() , il en découle
, il en découle ![]() . Nous pouvons alors reconsidérer l'équation régissant l'évolution de la pression totale en la formulant :
. Nous pouvons alors reconsidérer l'équation régissant l'évolution de la pression totale en la formulant :
![]()
Il s'avère alors que le membre de gauche ne peut dépendre que de ![]() alors que celui de droite ne peut dépendre que de
alors que celui de droite ne peut dépendre que de ![]() et
et ![]() . La conséquence est donc que les deux membres sont égaux à une même constante. Ceci permet de montrer que la pression totale varie linéairement avec
. La conséquence est donc que les deux membres sont égaux à une même constante. Ceci permet de montrer que la pression totale varie linéairement avec ![]() :
:
![]()
Remarque:
On notera que si la viscosité est négligée, la pression totale ne varie pas. En effet, la constante étant proportionnelle à ![]() , elle devient nulle, et on retrouve le contexte d'un écoulement de fluide parfait où l'équation de Bernoulli s'applique le long d'une ligne de courant :
, elle devient nulle, et on retrouve le contexte d'un écoulement de fluide parfait où l'équation de Bernoulli s'applique le long d'une ligne de courant :
![]()
on dit alors que la charge est constante ou bien encore qu'il n'y a pas de perte de charge.
En revanche, pour un fluide réel (dont la viscosité n'est pas négligeable), l'écoulement laminaire est caractérisé par une variation linéaire de la charge (ou pression totale) avec la distance parcourue. À ce stade, la logique peut déjà laisser supposer que la charge décroît et que par conséquent la constante est négative. En effet, puisque les frottements visqueux sont responsables d'une dissipation d'énergie et que la pression totale n'est autre qu'une énergie volumique, il s'ensuit logiquement que la pression totale doit diminuer avec la progression de l'écoulement (écoulement de Poiseuille).
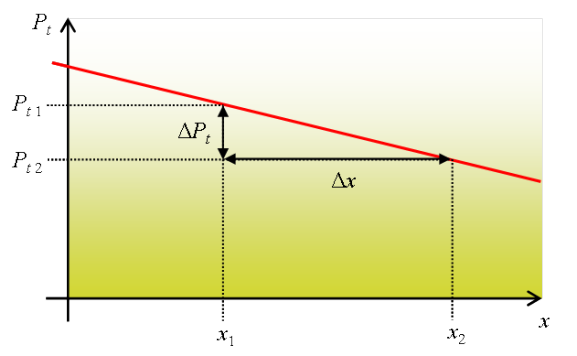
Dans l'hypothèse logique d'une pression totale diminuant linéairement avec la progression de l'écoulement, le graphe montre que sur une longueur![]() la chute de pression totale
la chute de pression totale ![]() est proportionnelle à
est proportionnelle à ![]() et s'exprime :
et s'exprime :
![]()
Ainsi, une chute de pression totale (perte de charge) se traduit par ![]() et est la conséquence d'un gradient de pression constant et négatif. C'est pourquoi on parle de pertes de charges régulières.
et est la conséquence d'un gradient de pression constant et négatif. C'est pourquoi on parle de pertes de charges régulières.
En pratique, la quantification de ces pertes de charge requiert la détermination du gradient de pression totale en fonction des paramètres caractérisant le fluide et l'écoulement. Après quoi, il est commode de généraliser l'équation de Bernoulli en y faisant apparaître les pertes de charges régulières de la manière suivante :
![]()
Pertes de charge en régime turbulent
En régime turbulent, le profil de vitesse dans une conduite cylindrique n’est plus parabolique ; à cause des turbulences, les vitesses sont uniformisées sur un large domaine. On observe une brusque variation de vitesse au voisinage des parois.

Les coefficients de perte de charge régulière λ devront être déterminés expérimentalement, ou bien tirés d’abaques, comme le diagramme de Moody reproduit ci-dessous, ou de lois empiriques.
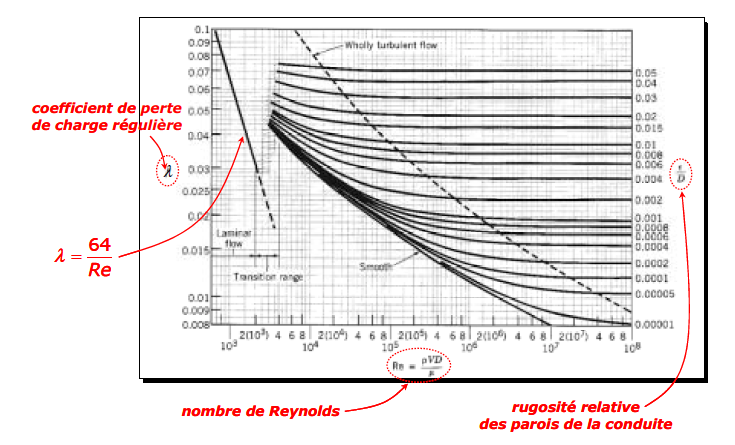
Les frottements exercés par le fluide sur les parois sont beaucoup plus importants en écoulement turbulent qu’en laminaire. En régime turbulent établi, l’essentiel des frottements est dû à l’existence d’une toute petite zone au voisinage des parois, appelée couche limite visqueuse, où les gradients de vitesse sont très élevés, donc où les phénomènes de viscosité jouent un très grand rôle.
Puisque les pertes de charge sont liées aux contraintes de frottement à la paroi de la conduite, elles dépendent non seulement des paramètres de l’écoulement, mais de l’état de surface (plus ou moins lisse ou rugueux) de cette paroi. On qualifie ordinairement cet état par une seule dimension géométrique ε, qui est d’un ordre de grandeur comparable à la hauteur géométrique moyenne des aspérités de cette paroi. Typiquement pour un tuyau en acier neuf ε = 0,03 à 0,1 mm.
Pertes de charge singulières.
La présence d’une singularité (d’un obstacle) sur l’écoulement dans une conduite comme un coude, un diaphragme, un élargissement brusque, une contraction, etc. crée un ΔP local appelé perte de charge singulière.
Dans la pratique industrielle, cette perte de charge est écrite sous la forme :
![]()
où le coefficient de perte de charge K, qui dépend de la géométrie et du nombre de Reynolds, est donné dans des formulaires appelés « dictionnaires de pertes de charge ». Quelques singularités typiques sont reproduites ci-dessous.
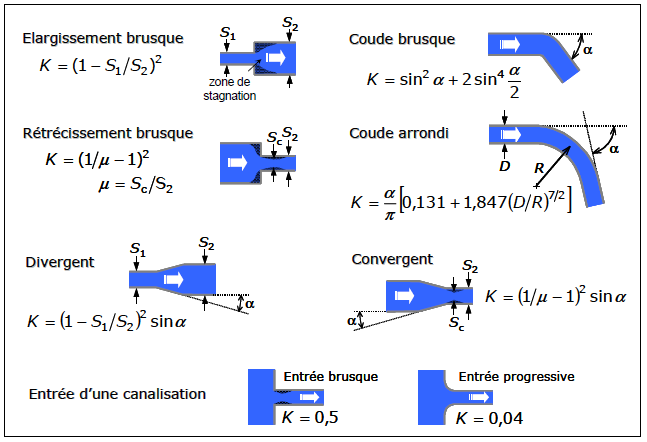
Dû à son inertie, le fluide ne suit pas complètement les changements brusques de direction : il se crée des zones de turbulences où il y a dissipation d’énergie. Ces zones, où le fluide est globalement stagnant, sont responsables des pertes de charge singulières.
On peut alors généraliser l’équation de Bernoulli :
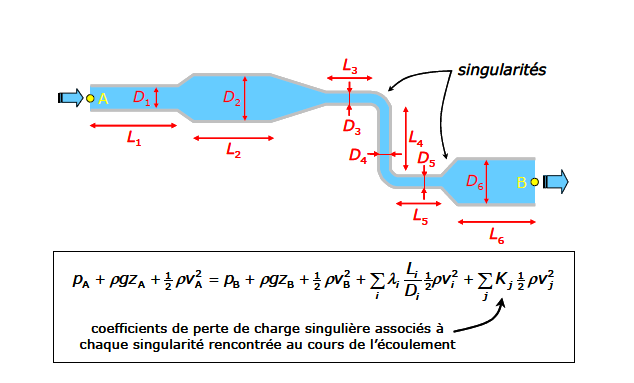
Coefficient de perte de charge.
Il est d'usage d'exprimer une perte de charge en fonction de la pression cinétique de l'écoulement dans la conduite. La pression cinétique est générée par le mouvement (elle correspond à l'énergie cinétique par unité de volume) et s'exprime : ![]() . La vitesse
. La vitesse ![]() peut être considérée comme la vitesse moyenne
peut être considérée comme la vitesse moyenne ![]() dans la conduite dans la mesure où la pression cinétique exprimée est aussi une valeur moyenne. Dans ces conditions, on peut formuler la perte de charge sur une longueur
dans la conduite dans la mesure où la pression cinétique exprimée est aussi une valeur moyenne. Dans ces conditions, on peut formuler la perte de charge sur une longueur ![]() d'une conduite de rayon
d'une conduite de rayon ![]() comme :
comme :
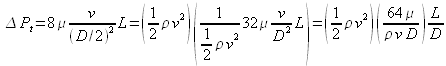
où apparaît le nombre de Reynolds caractérisant l'écoulement :
![]()
Ainsi, la perte de charge s'exprime :
![]()
où le rapport ![]() est un nombre sans dimension qui prend le nom de coefficient de perte de charge régulière. À partir de résultat, on peut généraliser cette formulation en exprimant toute perte de charge sur une longueur
est un nombre sans dimension qui prend le nom de coefficient de perte de charge régulière. À partir de résultat, on peut généraliser cette formulation en exprimant toute perte de charge sur une longueur ![]() de conduite de diamètre
de conduite de diamètre ![]() comme :
comme :
![]()
On met ainsi en évidence que les pertes de charge régulières sont proportionnelles à la pression cinétique, à une grandeur sans dimension ![]() caractérisant la conduite , et au coefficient de perte de charge régulière
caractérisant la conduite , et au coefficient de perte de charge régulière ![]() caractérisant l'écoulement et qui, lorsqu'il est laminaire (
caractérisant l'écoulement et qui, lorsqu'il est laminaire (![]() ), se formule comme
), se formule comme ![]() .
.
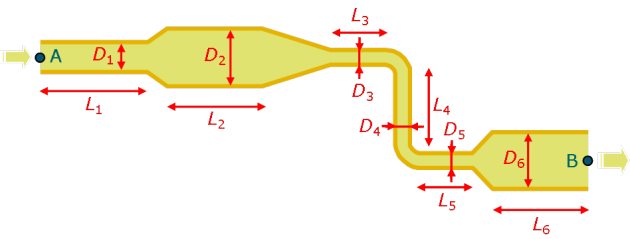
D'un point de vue pratique, cette formulation est particulièrement adaptée pour évaluer l'ensemble des pertes de charge occasionné par un circuit hydraulique comportant une succession de différents tronçons de conduite, comme l'illustre du schéma. La différence de pression totale entre l'entrée et la sortie du circuit est la somme de deux types de contribution :
-
les pertes de charge dues aux singularités que sont les changements de direction et les changements de diamètre (rétrécissements et élargissements) ;
-
les pertes de charge régulières dues aux frottements visqueux.
Les premières seront étudiées plus loin. Les secondes se formulent comme la somme des pertes occasionnées par chaque tronçon :
![]()